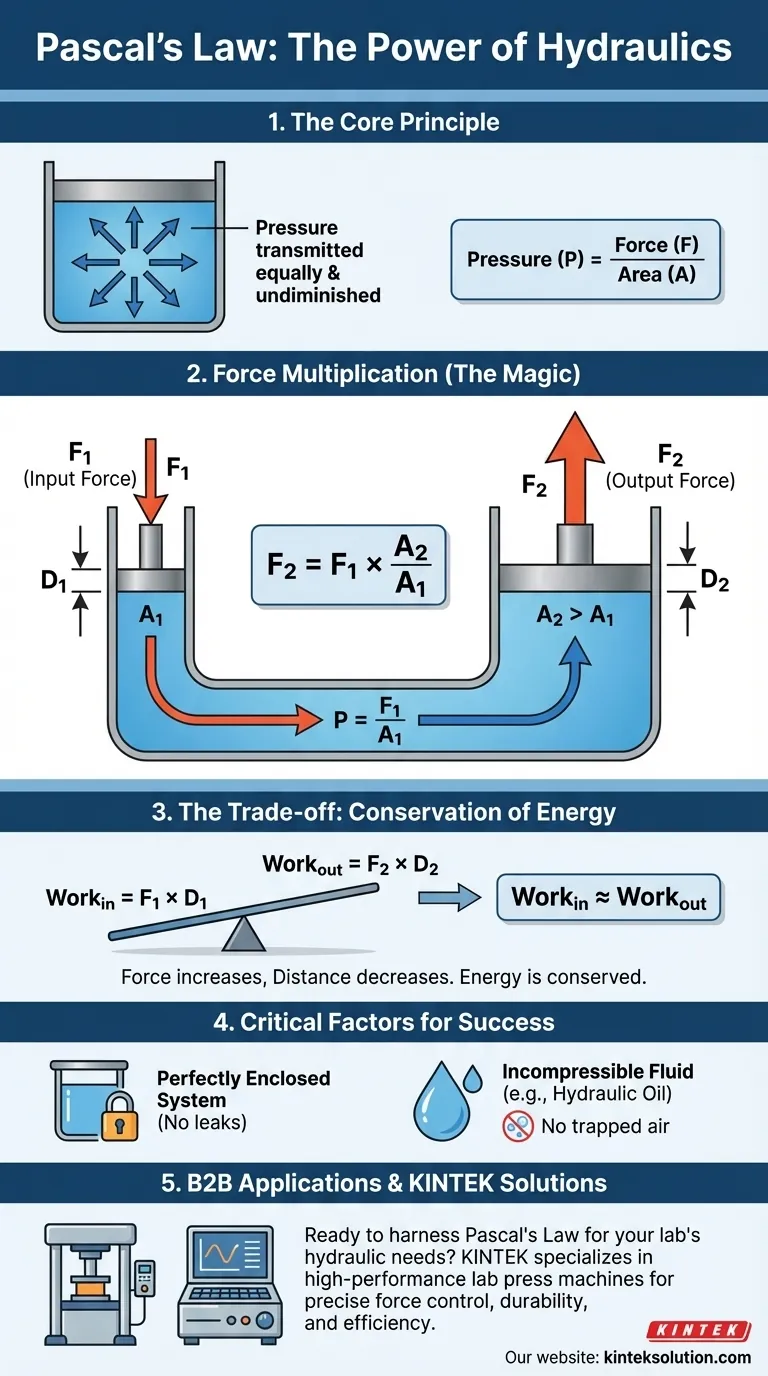
At its core, Pascal's Law states that a change in pressure at any point in an enclosed, incompressible fluid is transmitted equally and undiminished to all portions of that fluid. This means that if you push on a fluid in a sealed container, the pressure increases everywhere inside that container by the exact same amount, at the exact same time.
While the definition focuses on pressure transmission, the true power of Pascal's Law lies in how it allows us to achieve massive force multiplication. This single principle is the foundation of nearly all modern hydraulic systems.
The Fundamental Equation: Pressure, Force, and Area
To grasp the implications of Pascal's Law, you must first understand the relationship between its three core components.
Defining Pressure
Pressure (P) is defined as a Force (F) applied over a specific Area (A). The equation is P = F/A.
Think of the difference between someone pushing you with an open palm versus a single finger. The force might be the same, but the pressure from the fingertip is far greater because it's concentrated on a much smaller area.
The Role of an Incompressible Fluid
Pascal's Law relies on the use of an incompressible fluid, like water or hydraulic oil. When you apply force to this type of fluid, it doesn't get squeezed into a smaller volume.
Because the fluid cannot be compressed, the energy you introduce has to be transmitted elsewhere. This is how the pressure propagates instantly throughout the entire system.
The Magic of Force Multiplication
The true genius of applying Pascal's Law is not just that pressure is transmitted, but that it can be leveraged to multiply force. This is the operating principle behind everything from a car jack to the landing gear on an aircraft.
The Basic Hydraulic Model
Imagine a U-shaped tube filled with oil, sealed at both ends by pistons. One piston is small (the input piston), and the other is large (the output piston).
Applying the Input Force
Let's say you apply a small downward force (F1) to the small piston, which has an area of A1. This creates a pressure in the fluid: P = F1 / A1.
Transmitting the Pressure
According to Pascal's Law, this exact pressure (P) is now present everywhere in the fluid. This includes the area directly beneath the large output piston.
Calculating the Output Force
This same pressure (P) now pushes upward on the large piston, which has an area of A2. The resulting upward force (F2) is F2 = P x A2.
Because the pressure is the same throughout (F1/A1 = F2/A2), you can see that the output force is proportional to the ratio of the areas. If the output piston's area is 10 times larger than the input piston's area, the output force will be 10 times greater than the force you applied.
Understanding the Trade-offs
This force multiplication does not come from nowhere; it follows the laws of physics and involves critical compromises.
Conservation of Energy
You cannot create energy from nothing. While the output force is multiplied, the distance the output piston moves is proportionally reduced.
To lift the large piston by 1 inch, you may need to push the small piston down by 10 inches. The work done (Force x Distance) remains the same on both sides, ignoring friction.
The Importance of an "Enclosed" System
Pascal's principle only works in a perfectly sealed system. Any leak will cause the fluid to escape when pressure is applied, dissipating the pressure and leading to system failure.
Fluid Properties Matter
While we often assume an ideal, incompressible fluid, real-world hydraulic fluids have viscosity (resistance to flow) and can contain trapped air bubbles. Air is highly compressible, and its presence in hydraulic lines can make the system feel "spongy" and dramatically reduce its efficiency.
How to Apply This to Your Project
Understanding the principle allows you to design and troubleshoot systems effectively. Your specific goal will determine which aspect of the law is most important.
- If your primary focus is mechanical advantage: Concentrate on maximizing the area ratio between the output and input pistons (A2/A1) to achieve the desired force multiplication for a press or lifting jack.
- If your primary focus is system efficiency: Prioritize creating a perfectly sealed system and using a high-quality, incompressible fluid to minimize energy losses from leaks or internal compression.
- If your primary focus is precision control: Leverage the work trade-off; a small, manageable movement on the input can translate to a very small but powerful and precise movement on the output, which is ideal for systems like vehicle brakes.
By understanding this principle, you move from simply knowing a definition to grasping the elegant power behind all hydraulic engineering.
Summary Table:
| Aspect | Key Insight |
|---|---|
| Definition | Pressure change in incompressible fluid is transmitted equally and undiminished. |
| Force Multiplication | Output force increases with area ratio (F2 = F1 × (A2/A1)). |
| Trade-offs | Force gain reduces distance moved; energy is conserved. |
| Applications | Used in hydraulic jacks, presses, and precision control systems. |
Ready to harness Pascal's Law for your lab's hydraulic needs? KINTEK specializes in high-performance lab press machines, including automatic lab presses, isostatic presses, and heated lab presses. Our equipment ensures precise force control, durability, and efficiency for your laboratory applications. Contact us today to discuss how our solutions can optimize your projects and boost productivity!
