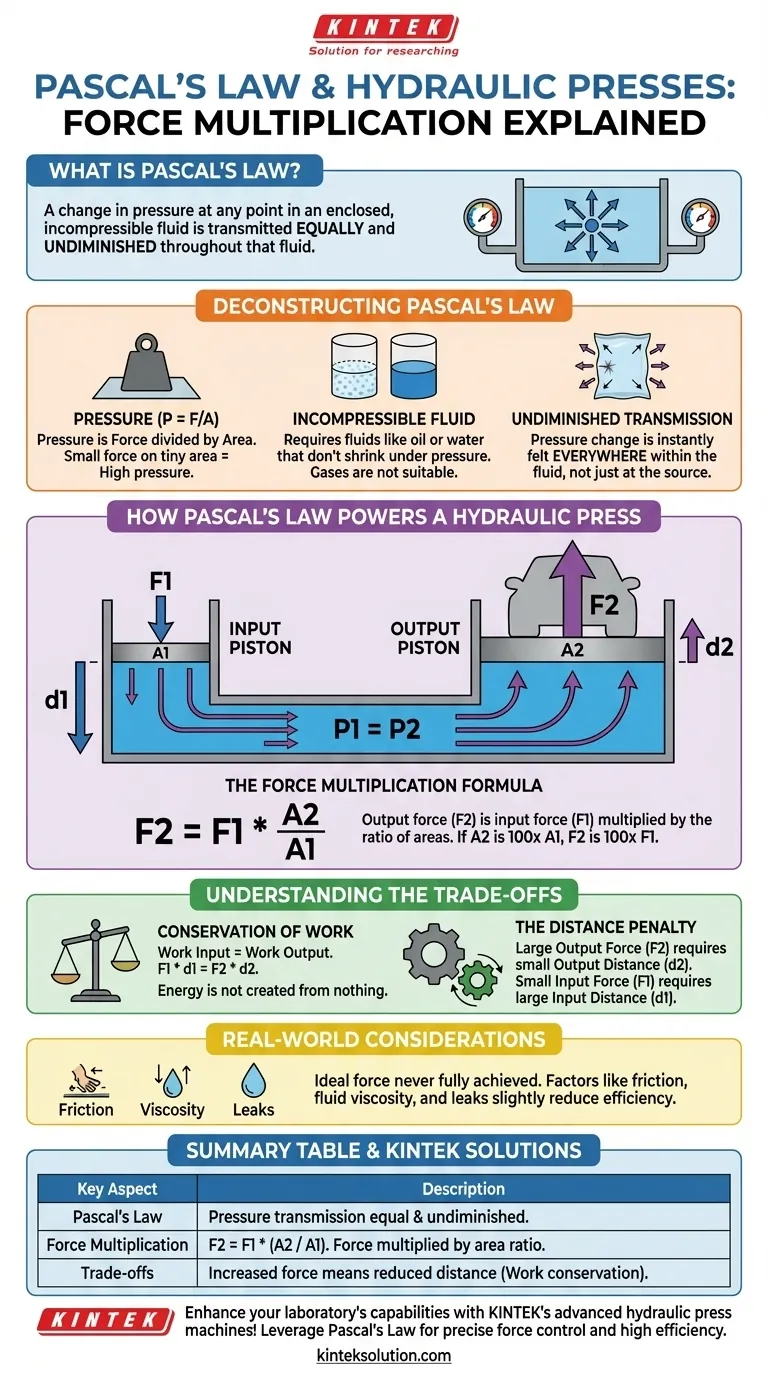
At its core, Pascal's Law states that a change in pressure at any point in an enclosed, incompressible fluid is transmitted equally and undiminished throughout that fluid. This principle is the fundamental mechanism behind hydraulic presses, allowing a small, manageable force to be converted into an immensely powerful one. It works by transmitting that initial pressure over a much larger area, thereby multiplying the resultant force.
The central insight of Pascal's Law is that you are not multiplying force out of thin air. Instead, you are using an incompressible fluid to transmit pressure uniformly, allowing a small force on a small area to generate an equivalent pressure that acts on a larger area, resulting in a larger total force.
Deconstructing Pascal's Law
To truly grasp how hydraulic systems work, we must first understand the three core components of the principle itself.
The Definition of Pressure
Pressure (P) is defined as a force (F) applied over a specific area (A). The relationship is expressed by the foundational equation P = F/A.
A small force concentrated on a tiny area can generate the same pressure as a massive force spread out over a large area. This concept is key to understanding force multiplication.
The Incompressible Fluid
Pascal's Law requires an incompressible fluid, such as oil or water. This means the fluid's volume does not noticeably decrease when pressure is applied.
Gases are compressible, so they would simply compact under pressure instead of transmitting it efficiently, making them unsuitable for this application.
Undiminished Transmission
This is the most critical aspect of the law. When you apply pressure to any part of the confined fluid, that exact same pressure is instantly felt everywhere within the fluid.
Think of a sealed plastic bag full of water. If you poke it with your finger in one spot, the entire bag becomes taut and pressure increases equally throughout, not just where your finger is.
How Pascal's Law Powers a Hydraulic Press
A hydraulic press is the classic, practical application of this principle. It uses a simple two-piston system to achieve significant force multiplication.
The Two-Piston System
A basic hydraulic system consists of two cylindrical pistons connected by a pipe filled with an incompressible fluid.
- Piston 1 (Input): Has a small surface area (
A1). - Piston 2 (Output): Has a much larger surface area (
A2).
A small input force (F1) is applied to Piston 1, creating a pressure in the fluid.
Equal Pressure, Unequal Force
According to Pascal's Law, the pressure created by the input piston (P1 = F1 / A1) is transmitted undiminished throughout the fluid. This means the pressure acting on the output piston (P2) is exactly the same.
Therefore, P1 = P2.
Because P = F/A, we can substitute to get the equation: F1 / A1 = F2 / A2.
The Force Multiplication Formula
By rearranging the equation, we can solve for the output force (F2):
F2 = F1 * (A2 / A1)
This elegantly demonstrates the multiplication effect. The output force is the input force multiplied by the ratio of the areas of the two pistons. If the output piston's area is 100 times larger than the input piston's area, the force is multiplied by 100.
Understanding the Trade-offs
This principle does not create energy from nothing. The amplified force comes at a cost, which is governed by the law of conservation of energy.
The Conservation of Work
In physics, Work = Force x Distance. For a hydraulic system to be in equilibrium, the work done on the input piston must equal the work done by the output piston.
Work_input = Work_output
F1 * d1 = F2 * d2
The Distance Penalty
Since the output force (F2) is much larger than the input force (F1), the distance the output piston moves (d2) must be proportionally smaller than the distance the input piston moves (d1).
To lift a heavy car by one inch with the large piston, you may have to push the small piston a distance of several feet. You trade movement distance for force multiplication.
Real-World Inefficiencies
In any practical application, the ideal output force is never fully achieved. Factors like friction between the pistons and cylinder walls, fluid viscosity, and potential leaks in the system will all slightly reduce the efficiency of the force transmission.
Making the Right Choice for Your Goal
Understanding this principle allows you to make targeted design decisions based on your primary objective.
- If your primary focus is maximum force multiplication: You must maximize the ratio of the output area (
A2) to the input area (A1). - If your primary focus is operational speed: You must accept a lower force multiplication ratio, as a higher output distance (
d2) requires a smaller area ratio (A2/A1). - If you are designing a real-world system: Always factor in a margin for inefficiency; the actual output force will be slightly less than the theoretical calculation due to friction and other losses.
Ultimately, Pascal's Law provides a powerful and elegant framework that remains a cornerstone of modern mechanical and industrial engineering.
Summary Table:
| Key Aspect | Description |
|---|---|
| Pascal's Law | Pressure change in an incompressible fluid is transmitted equally and undiminished throughout the fluid. |
| Force Multiplication Formula | F2 = F1 * (A2 / A1), where F2 is output force, F1 is input force, A2 is output area, A1 is input area. |
| Trade-offs | Increased force comes with reduced distance moved, governed by conservation of energy (F1 * d1 = F2 * d2). |
| Applications | Ideal for hydraulic presses in labs, offering precise control and high force for material testing and processing. |
Enhance your laboratory's capabilities with KINTEK's advanced hydraulic press machines! Whether you need an automatic lab press, isostatic press, or heated lab press, our equipment leverages Pascal's Law to deliver precise force control, high efficiency, and reliable performance for all your lab needs. Don't let inefficiencies hold you back—contact us today to discover how our solutions can boost your productivity and achieve superior results in material testing and processing!
