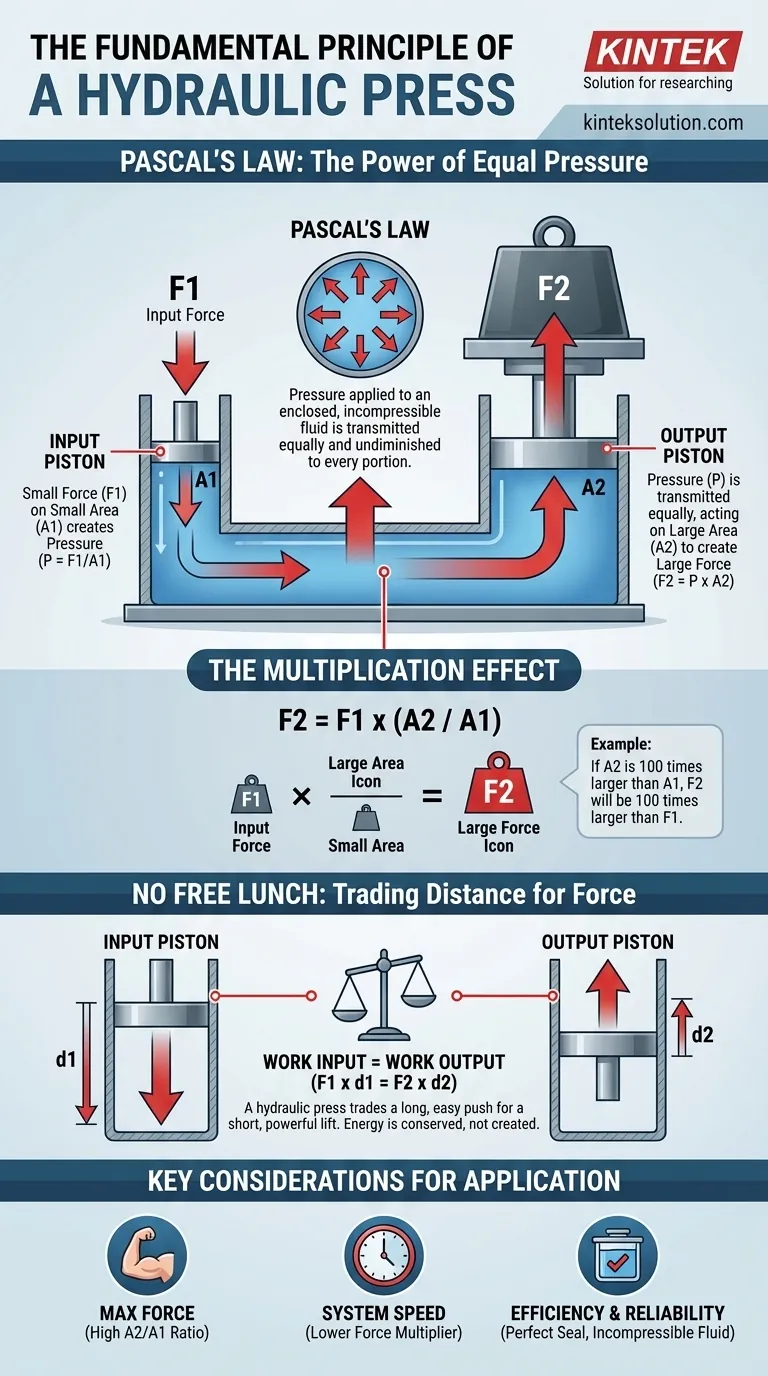
The fundamental principle is Pascal's Law, which allows for immense force multiplication. This law states that pressure applied to an enclosed, incompressible fluid is transmitted equally and undiminished to every portion of the fluid and the walls of its container. In a hydraulic press, this means a small force applied to a small area generates a pressure that, when acting on a larger area, produces a proportionally larger output force.
A hydraulic press does not create energy, but rather trades distance for force. By applying a small force over a long distance on a small piston, you generate an immense force that moves a very short distance on a large piston, all thanks to the uniform pressure of the confined fluid.
Unpacking Pascal's Law
The operation of a hydraulic press feels almost magical, but it hinges on three distinct concepts working in unison: a confined fluid, the definition of pressure, and the principle of equal transmission.
The Role of the Confined Fluid
A hydraulic system is a closed loop, typically filled with an incompressible fluid like oil. "Incompressible" is the key property; it means the fluid's volume does not noticeably decrease under pressure.
Because the fluid cannot be squeezed into a smaller space, any force applied to it is immediately converted into pressure that seeks to act on the entire container.
Pressure: The Great Equalizer
Pressure is defined as Force divided by Area (P = F/A). It is not force itself, but the distribution of that force over a surface.
Imagine the difference between being stepped on by a flat shoe versus a stiletto heel. The force (your weight) is the same, but the tiny area of the stiletto concentrates that force into immense pressure. Pascal's Law leverages this exact relationship.
Equal and Undiminished Transmission
This is the core of Pascal's Law. When you apply pressure to one part of the confined fluid, that exact amount of pressure is instantly available everywhere else within the system.
Think of a sealed plastic bag full of water. If you poke it with your finger in one spot, the entire bag becomes taut. The pressure you applied isn't just felt under your finger; it's transmitted equally to all inside surfaces of the bag.
The Mechanics of Force Multiplication
The genius of the hydraulic press is its use of two pistons with different surface areas to exploit Pascal's Law and create a mechanical advantage.
The Input Piston (Small Force, Small Area)
The process begins at the smaller piston, often called the effort piston. A modest input force (F1) is applied to its small surface area (A1).
This action generates a specific pressure within the fluid: P = F1 / A1.
The Output Piston (Large Force, Large Area)
This pressure is transmitted, undiminished, throughout the fluid. It now pushes against the bottom of the much larger output piston, which has a surface area of A2.
Because the pressure is the same everywhere, the force exerted on the output piston (F2) is equal to that pressure multiplied by the larger area: F2 = P x A2.
The Multiplication Effect
By substituting the first equation into the second, we get the relationship: F2 = (F1 / A1) x A2.
This can be simplified to F2 = F1 x (A2 / A1). The term (A2 / A1) is the force multiplication factor. If the output piston has 100 times the surface area of the input piston, the output force will be 100 times the input force.
Understanding the Trade-offs: No Free Lunch
The massive force amplification of a hydraulic press can seem like it violates the laws of physics, but it does not. The system is governed by the conservation of energy.
The Law of Conservation of Energy
A hydraulic press cannot create more energy than is put into it. It is a force multiplier, not an energy multiplier.
The Work-Distance Relationship
Work is defined as Force multiplied by Distance (W = F x d). Ignoring minimal losses from friction, the work done on the input piston must equal the work performed by the output piston.
Therefore, F1 x d1 = F2 x d2.
Trading Distance for Force
Since we know the output force (F2) is much larger than the input force (F1), the output distance (d2) must be proportionally smaller than the input distance (d1).
To lift a heavy car one inch using the large piston, you may have to push the small piston down several feet. You are trading a long, easy push for a short, powerful lift.
Making the Right Choice for Your Application
Applying this principle requires understanding how changing one variable affects the others.
- If your primary focus is maximum force output: Prioritize maximizing the area ratio between the output and input pistons (A2/A1). A larger ratio directly translates to a higher force multiplier.
- If your primary focus is system speed: You must accept a lower force multiplication. A smaller area ratio means the output piston will travel a greater distance for each stroke of the input piston.
- If your primary focus is efficiency and reliability: Ensure the system is perfectly sealed to prevent fluid leaks, which cause pressure loss. Use a high-quality, incompressible hydraulic fluid to guarantee that input force is translated directly into pressure.
Ultimately, designing or using a hydraulic system is an exercise in balancing this fundamental trade-off between force and distance to achieve your specific goal.
Summary Table:
| Concept | Key Insight | Application in Hydraulic Press |
|---|---|---|
| Pascal's Law | Pressure in a confined fluid is transmitted equally and undiminished | Enables force multiplication through piston area ratios |
| Force Multiplication | Output force = Input force × (Area ratio) | Achieves high forces for tasks like material testing in labs |
| Energy Conservation | Work input equals work output (F1 × d1 = F2 × d2) | Ensures no energy creation, only force-distance trade-off |
| Fluid Properties | Incompressible fluids like oil maintain pressure integrity | Critical for reliable operation in laboratory environments |
Ready to enhance your laboratory's capabilities with reliable hydraulic presses? KINTEK specializes in lab press machines, including automatic lab presses, isostatic presses, and heated lab presses, designed to deliver precise force control and efficiency for your research and testing needs. Our equipment leverages principles like Pascal's Law to ensure optimal performance, helping you achieve accurate results in material compression, molding, and more. Contact us today to discuss how our solutions can support your specific applications and boost your lab's productivity!
