What Are Matrix Effects In Xrf Quantification? Master Accurate Elemental Analysis With Proven Correction Methods

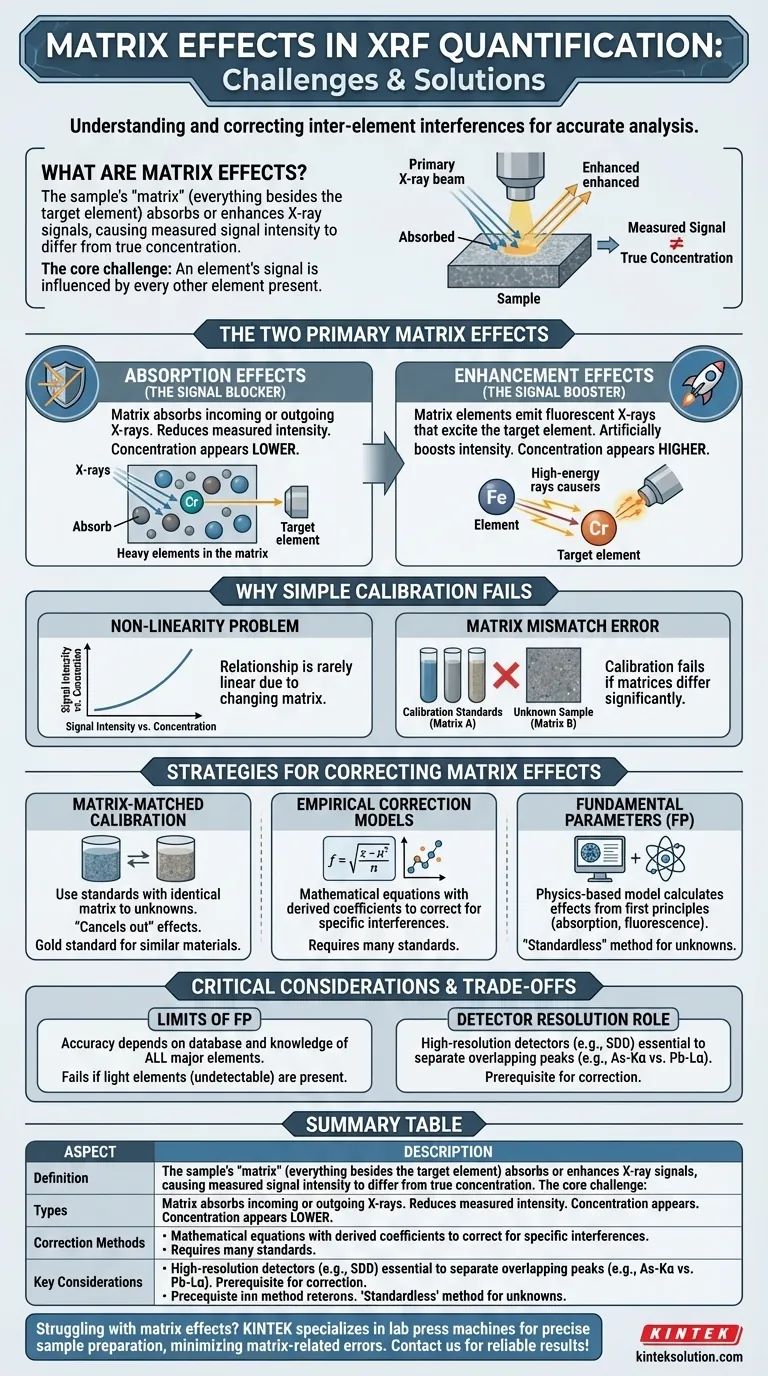
In X-ray fluorescence (XRF) analysis, matrix effects are inter-element interferences within a sample that cause the measured signal of an element to be different from its true concentration. The "matrix"—which is everything in the sample besides the specific element being measured—can absorb or enhance the X-ray signals, leading to significant errors in quantification if not properly corrected.

The core challenge of XRF is that an element's signal is not independent; it is influenced by every other element present. Accurately overcoming these matrix effects requires either using perfectly matched calibration standards or employing sophisticated software models to mathematically correct for these physical interactions.

The Two Primary Types of Matrix Effects

Matrix effects are not random errors. They are predictable physical phenomena that primarily fall into two categories: absorption and enhancement.

Absorption Effects (The Signal Blocker)

The most common matrix effect is absorption. The sample matrix can absorb both the incoming X-rays from the source and the outgoing fluorescent X-rays from the element of interest.

This happens in two ways. First, heavy elements in the matrix can absorb the primary X-rays, reducing the number that reach and excite your target element. Second, the matrix can absorb the characteristic X-rays emitted by your target element before they ever reach the detector. Both effects reduce the measured intensity, making the element's concentration appear lower than it actually is.

Enhancement Effects (The Signal Booster)

Enhancement, or secondary fluorescence, is the opposite of absorption. This occurs when a different element in the matrix gives off fluorescent X-rays with enough energy to excite your target element.

For example, if you are measuring Chromium (Cr) in a steel alloy, the high-energy fluorescent X-rays from Iron (Fe) can cause the Cr atoms to fluoresce as well. This "extra" fluorescence adds to the signal produced by the primary X-ray source, artificially boosting the Cr intensity and making its concentration appear higher than it truly is.

Why Simple Calibration Is Not Enough

These physical effects directly undermine basic quantitative methods, where one assumes that signal intensity is directly proportional to concentration.

The Problem of Non-Linearity

Because of matrix effects, the relationship between an element's concentration and its measured X-ray intensity is rarely a straight line. Doubling the amount of an element will not necessarily double its signal if the matrix is also changing. This non-linearity makes simple calibration curves unreliable for samples with varying compositions.

The "Matrix Mismatch" Error

This is the most common practical pitfall. If you create a calibration curve using a set of standards with one matrix type (e.g., simple metal alloys), that calibration will produce inaccurate results when used to measure a sample with a different matrix (e.g., a mineral ore, a plastic, or an oil). The absorption and enhancement effects will be completely different between the two sample types, invalidating the calibration.

Strategies for Correcting Matrix Effects

Fortunately, there are well-established methods to compensate for these effects and achieve accurate quantitative analysis.

Matrix-Matched Calibration

This is the most direct solution. It involves creating calibration standards where the matrix is nearly identical to that of the unknown samples. This method effectively "cancels out" the matrix effects because they are the same in both the standards and the unknowns. It is the gold standard for accuracy but is only practical for routine analysis of very similar materials.

Empirical Correction Models

These models use mathematical equations with empirically derived coefficients to correct for the influence of specific interfering elements. They require analyzing a large number of well-characterized standards to build a robust model, but once established, they can be very effective for a defined range of material types.

Fundamental Parameters (FP) Approach

The Fundamental Parameters (FP) method is the most powerful and flexible approach. Instead of relying on standards, FP uses a physics-based model to calculate the matrix effects from first principles. The software uses fundamental constants—like absorption coefficients and fluorescence yields—to predict how X-rays will interact with the composition of the sample. This "standardless" method is ideal for analyzing unknown or highly variable samples where creating matched standards is impossible.

Understanding the Trade-offs and Pitfalls

While correction methods are powerful, they have limitations that are critical to understand for reliable analysis.

The Limits of Fundamental Parameters

The FP approach is not infallible. Its accuracy depends on the quality of its physics database and, critically, on the assumption that the software knows about all major elements in the sample. If a significant portion of the matrix is made of light elements (like Carbon, Oxygen, or Nitrogen) that the XRF cannot detect, the FP model will be based on an incomplete picture and its corrections will be inaccurate.

The Role of Detector Resolution

Before you can correct for matrix effects, you must be able to cleanly measure an element's signal. This can be compromised by poor detector resolution, which causes spectral peak overlaps. For instance, the Arsenic (As) K-alpha peak is very close to the Lead (Pb) L-alpha peak. A low-resolution detector cannot separate them, making it impossible to get an accurate intensity for either one.

Modern, high-resolution detectors like Silicon Drift Detectors (SDDs) are essential for separating these overlapping peaks. Accurate peak identification is a prerequisite for any successful matrix correction.

Choosing the Right Approach for Your Analysis

Your analytical goal dictates the best strategy for handling matrix effects.

If your primary focus is quality control on a known material: Matrix-matched standards provide the highest accuracy and repeatability.
If your primary focus is analyzing diverse and unknown samples: The Fundamental Parameters (FP) approach offers the most flexibility and is often the only practical option.
If you are measuring trace elements next to major elements: Ensure your system has a high-resolution detector to prevent peak overlaps before even considering matrix correction.

Understanding and correcting for matrix effects is the key to transforming XRF from a qualitative screening tool into a precise quantitative instrument.

Summary Table:

Aspect	Description
Definition	Inter-element interferences in XRF that alter signal intensity from true concentration.
Types	Absorption (reduces signal) and Enhancement (boosts signal).
Correction Methods	Matrix-matched calibration, Empirical models, Fundamental Parameters (FP).
Key Considerations	Requires high-resolution detectors for accurate peak separation and complete element knowledge for FP.

Struggling with matrix effects in your XRF analysis? KINTEK specializes in lab press machines, including automatic, isostatic, and heated lab presses, designed to support precise sample preparation for accurate XRF quantification. Our equipment helps minimize matrix-related errors by ensuring uniform sample consistency, leading to reliable results in quality control and research. Let us enhance your laboratory's efficiency—contact us today to discuss how our solutions can benefit your specific needs!