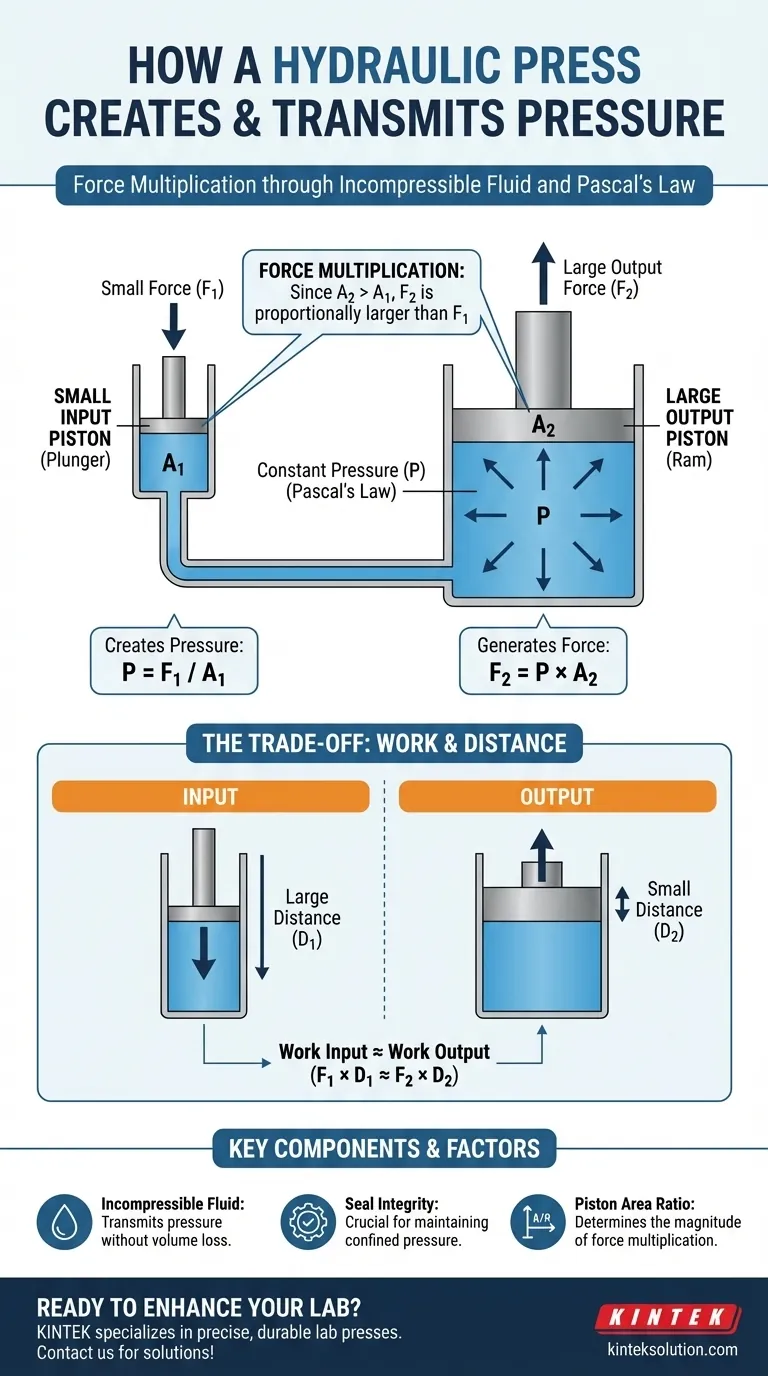
At its core, a hydraulic press creates force multiplication by using an incompressible fluid to transfer pressure. A small force applied to a small piston generates pressure throughout the fluid. This same pressure then acts on a much larger piston, generating a proportionally larger output force.
The power of a hydraulic press does not come from creating pressure, but from transmitting it. Based on Pascal's Law, the constant pressure within the confined fluid allows a small input force on a small area to be converted into a massive output force on a large area.
The Core Principle: Pascal's Law Explained
To truly understand a hydraulic press, you must first understand the fundamental law of physics that governs it. This isn't a mechanical trick; it's a fluid dynamics principle.
What is Pascal's Law?
Pascal's Law states that a pressure change at any point in a confined, incompressible fluid is transmitted equally throughout the fluid.
Think of it like squeezing a sealed water bottle. The pressure you apply with your hand isn't just felt where you're squeezing; it increases everywhere inside the bottle simultaneously.
The Role of the Incompressible Fluid
Hydraulic systems use specific fluids, like oil, precisely because they are incompressible. Unlike a gas, a liquid's volume does not noticeably decrease under pressure.
Instead of being squeezed, the fluid acts as a solid medium for transferring force from one point to another. This is a critical distinction; the fluid is not being compressed to create pressure, it is being contained to transmit it.
Pressure vs. Force: The Critical Distinction
The most common point of confusion is the relationship between pressure and force. The formula is simple: Pressure = Force / Area.
In a hydraulic press, the pressure is the constant. The force is the variable. A small force applied over a small area creates the exact same pressure as a large force acting over a large area. The press exploits this relationship.
How Force Is Multiplied in Practice
The design of a hydraulic press is a direct physical application of Pascal's Law, using two pistons of different sizes to manipulate the relationship between force and area.
The Input Piston (The Plunger)
First, an operator applies a modest input force (F1) to a small piston with a small area (A1).
This action creates a specific pressure (P) within the hydraulic fluid, calculated as P = F1 / A1.
The Output Piston (The Ram)
Because of Pascal's Law, this exact same pressure (P) is now exerted on every surface inside the system, including the face of the much larger output piston, or ram.
This piston has a large area (A2). The resulting output force (F2) is therefore F2 = P * A2. Because A2 is much larger than A1, F2 becomes much larger than the initial input force, F1. This is force multiplication.
Understanding the Trade-offs
This force multiplication does not come for free. The laws of physics, specifically the conservation of energy, demand a compromise.
The "No Free Lunch" Principle: Work and Distance
While you gain a massive advantage in force, you pay a price in distance. The amount of work done on the input piston must equal the work done by the output piston (ignoring minor efficiency losses).
Since Work = Force x Distance, the small input piston must travel a much longer distance to move the large output piston even a small amount. To lift the ram by one inch, the plunger might have to be pumped for a distance of many inches or feet.
System Inefficiencies
In the real world, no system is perfectly efficient. A small amount of energy is always lost.
Friction between the piston seals and the cylinder walls, as well as the potential for microscopic fluid leaks, will slightly reduce the actual output force compared to the theoretical calculation.
Making the Right Choice for Your Application
Understanding the core principles allows you to evaluate a hydraulic system based on your specific goals.
- If your primary focus is maximum force multiplication: The key is to maximize the ratio between the output piston's area and the input piston's area.
- If your primary focus is speed of operation: Be aware that a higher force multiplication ratio will result in a slower output ram, as more fluid volume must be displaced by the input piston for each inch of movement.
- If your primary focus is system reliability: The integrity of the seals and the purity of the hydraulic fluid are paramount, as Pascal's Law only functions perfectly in a truly confined and incompressible system.
Mastering the interplay of pressure, force, and area is the key to effectively applying and troubleshooting any hydraulic system.
Summary Table:
| Component | Role in Pressure Transmission | Key Principle |
|---|---|---|
| Input Piston | Applies small force to create pressure | Pascal's Law: Pressure is transmitted equally |
| Hydraulic Fluid | Transmits pressure without compression | Incompressibility ensures force transfer |
| Output Piston | Generates large output force | Force = Pressure × Area (multiplication) |
Ready to enhance your lab's capabilities with reliable hydraulic presses? KINTEK specializes in lab press machines, including automatic, isostatic, and heated models, designed to deliver precise force control and durability for your laboratory needs. Contact us today to discuss how our solutions can optimize your processes and boost efficiency!
